Геометрический смысл производной связан - Лекции по динамике

Применение производной в математике разнообразно и широко используется в различных областях, включая изучение функций, решение задач математики, физики и других наук. Производная функции в точке характеризует скорость изменения функции в этой точке, что делает ее важным понятием дифференциального исчисления. Производная функции широко применяется при изучении скорости различных процессов. Вычисление производной применяется для исследования функций и является одной из задач математики.

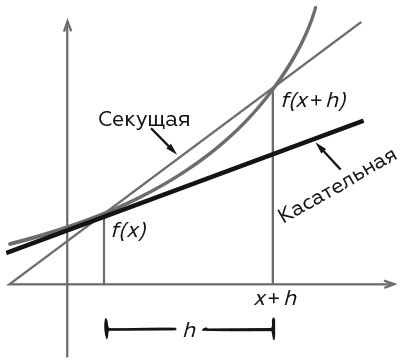
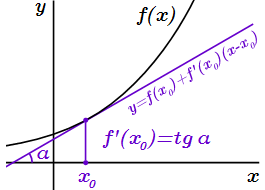
Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной

Математика от Геннадича. Уравнение касательной. Геометрический смысл производной. Производная функции является мощным инструментом при определении свойств функций, закономерностей и практических процессов. В данном видеоролике показаны некоторые виды сложных задач, решение которых связано с нахождением производных функций

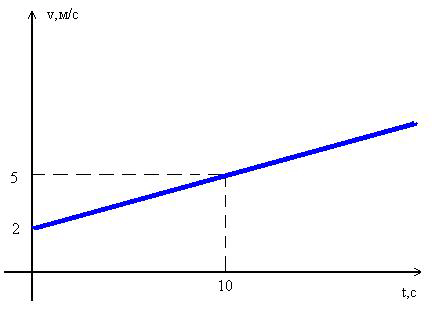
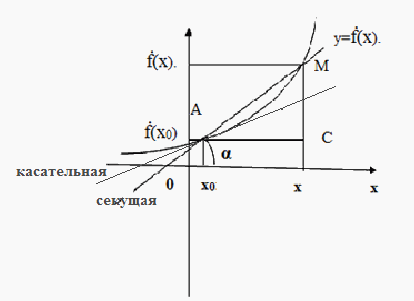
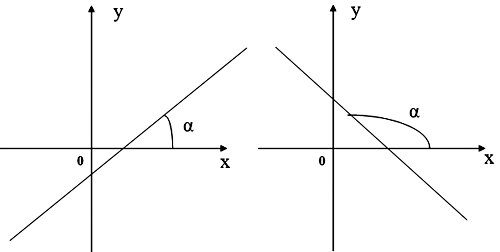
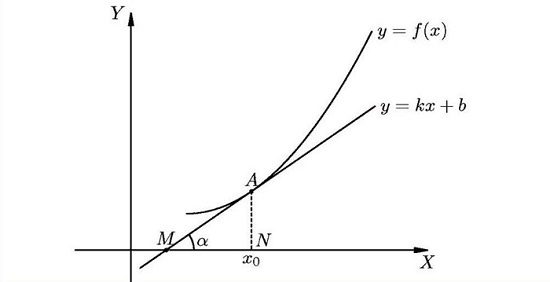
Согласны ли вы с утверждением? Касательная — это прямая, имеющая с данной кривой одну общую точку. Алгоритм 1.

Разделы: Математика. Учащиеся должны знать : что называется угловым коэффициентом прямой; углом между прямой и осью Ох; в чем состоит геометрический смысл производной; уравнение касательной к графику функции; способ построения касательной к параболе; уметь применять теоретические знания на практике. Задачи урока :.

Похожие статьи

• Наказание связанной - Отдельные аспекты защиты по уголовным делам, связанным с
• Как связать кофту с пуговицами регланом
• Все слова связанные с жизнью - Русский язык
• Вязанные вещи из мохера со схемами - Из мохера (коллекция вязаных идей схемы) - 2 - Вязание